Les parcours pédagogiques sont des ensembles d’ateliers qui permettent d’aborder différents aspects d’une même thématique. Ils sont prévus pour des groupes effectuant des visites au sein des Espaces Terra Numerica pour une durée de deux ou trois heures. Certains parcours peuvent être déclinés en mallettes pédagogiques qui sont mises à disposition des établissements scolaires afin d’expérimenter les sciences du numérique tout au long de l’année. Ce sont des parcours pédagogiques portables qui peuvent être déployés très facilement. Les premiers parcours pédagogiques sont décrits ci-dessous.
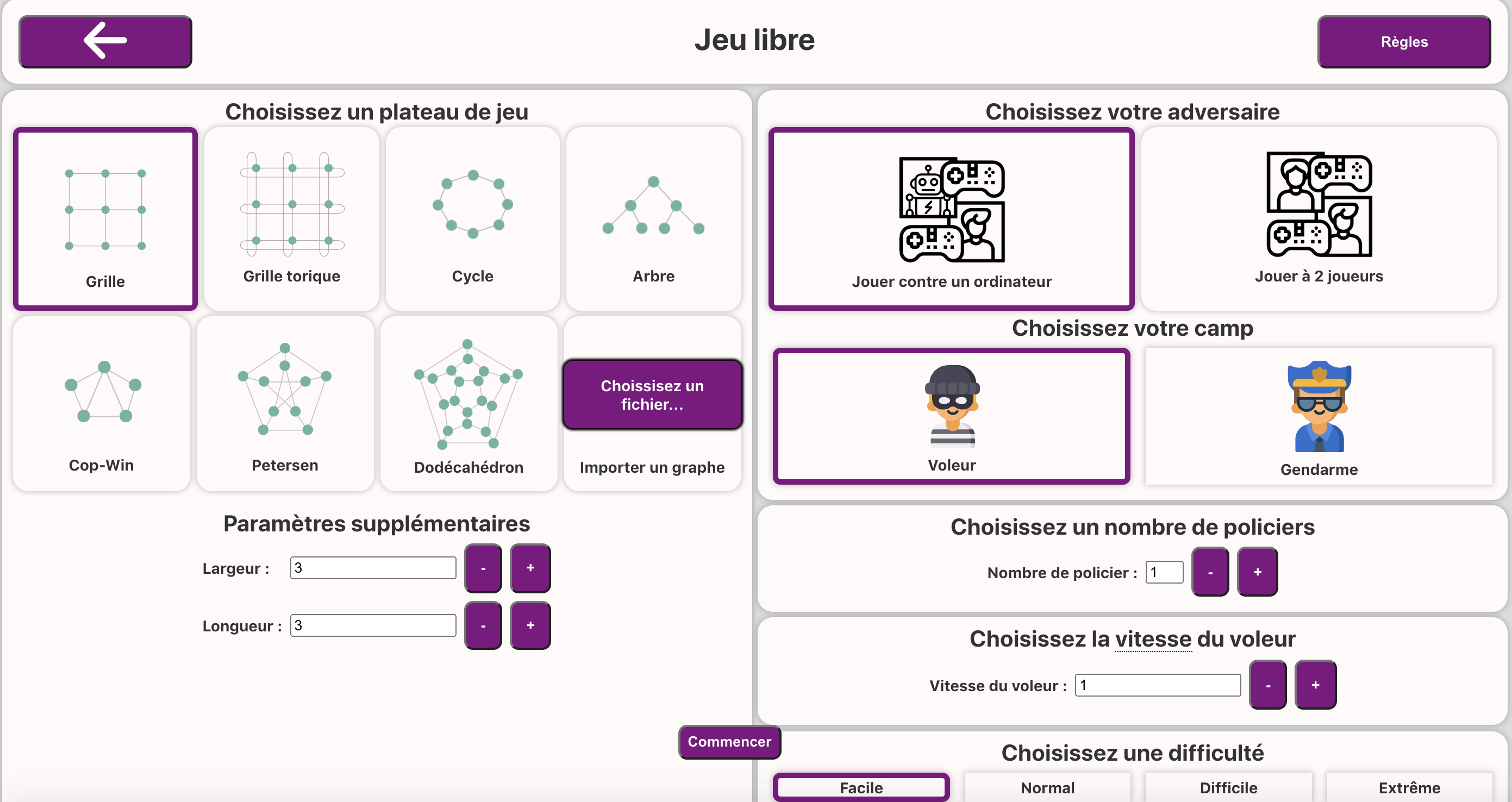
Jeux et intelligence artificielle
Ce parcours a pour but d’expliquer pourquoi et comment les ordinateurs gagnent aux jeux. Au travers de jeux combinatoires simples, certains ateliers permettent de se familiariser avec les notions de stratégies gagnantes et les notions d’invariants. D’autres ateliers renforcent cela avec cette fois un jeu asymétrique (les objectifs des deux joueurs sont de nature différente) qui modélise le problème de pré-téléchargement de page Web, donnant ainsi un exemple d’utilité des jeux. De plus, un atelier permet, tout en s’initiant au « reverse engineering » de mieux comprendre la notion de position forte ou faible à des jeux comme les échecs et d’appréhender les idées classiques pour développer des logiciels jouant (et gagnant) à ces jeux. Le reste du parcours est composé d’un atelier qui explique comment un ordinateur trouve une stratégie gagnante pour un jeu à l’aide de l’Intelligence Artificielle et plus précisément de l’apprentissage par renforcement. Enfin, un dernier atelier montre la limitation (actuelle) des algorithmes (y compris ceux d’intelligence artificielle) et comment certains puzzles résistent encore aux ordinateurs.
Niveau recommandé : à partir du cycle 3.
 Jeu des bâtonnets et jeu de Nim  Jeu du Web surfeur – version plateau |
 Tablette empoissonnée  Jeu du Web surfeur – grandeur nature |
 IA pour gagner au jeu de Nim  Un puzzle qui résiste aux ordinateurs |
 Algorithmes pour les échecs |
Robotique
Ce parcours regroupe un ensemble d’ateliers autour des robots. Plusieurs variantes du parcours peuvent être proposées en fonction de la nature souhaitée (débranchée ou branché par exemple) ou de la durée de la session par exemple. L’atelier Robotination a une durée de l’ordre de l’heure.
Niveau recommandé : à partir du cycle 3.
 Thymio Race  CreaCube |
 Apprentissage pour la stabilisation d’un pendule |
 TaxiBot  Robotination |
 Youpi 2.0  Nono |
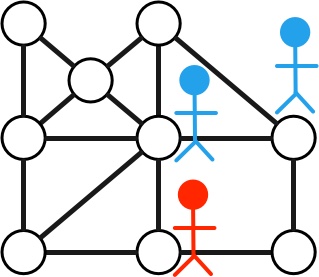
Réseaux
La thématique de ce parcours est celle des réseaux. Les ateliers disponibles sont proposés en grandeur nature (supports cerceaux et lattes, réseaux de trains). Plusieurs variantes du parcours peuvent ainsi être proposées en fonction de l’espace dédié par exemple. D’autres ateliers (sur d’autres supports) sont en cours de réalisation.
Niveau recommandé : à partir du cycle 3.
 Plus court chemin – grandeur nature  Planification de tournées |
 Plus court chemin – avec des trains |
 IA pour le voyageur de commerce |
 Optimisation des bus scolaires |
Trois millions de dollars
Ce parcours propose de découvrir des problèmes (jeux) simples à expliquer mais difficiles à résoudre. Faire autrement que tester toutes les possibilités pour trouver une solution nous ferait devenir riche. Mais personne ne sait si cela est possible…
Niveau recommandé : à partir du cycle 3.
|
Jeu du Web surfeur – version plateau |
Jeu du Web surfeur – grandeur nature |
Un puzzle qui résiste aux ordinateurs |
IA pour le voyageur de commerce |
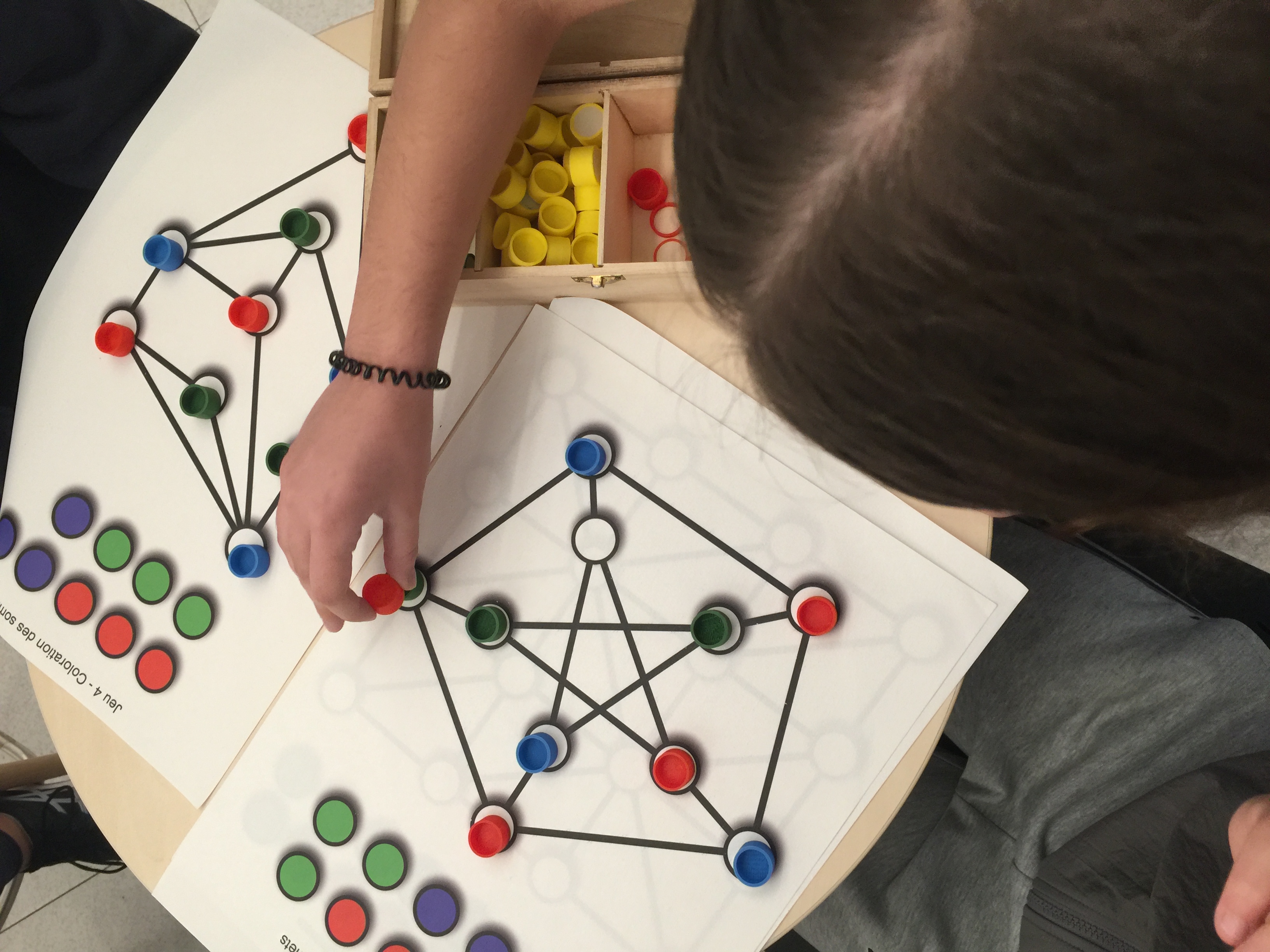
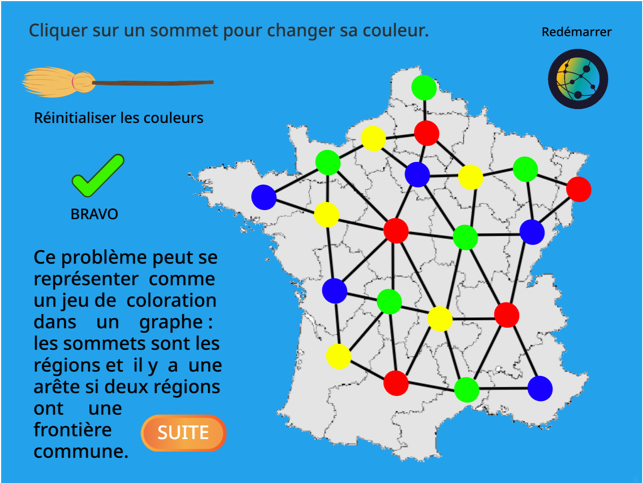
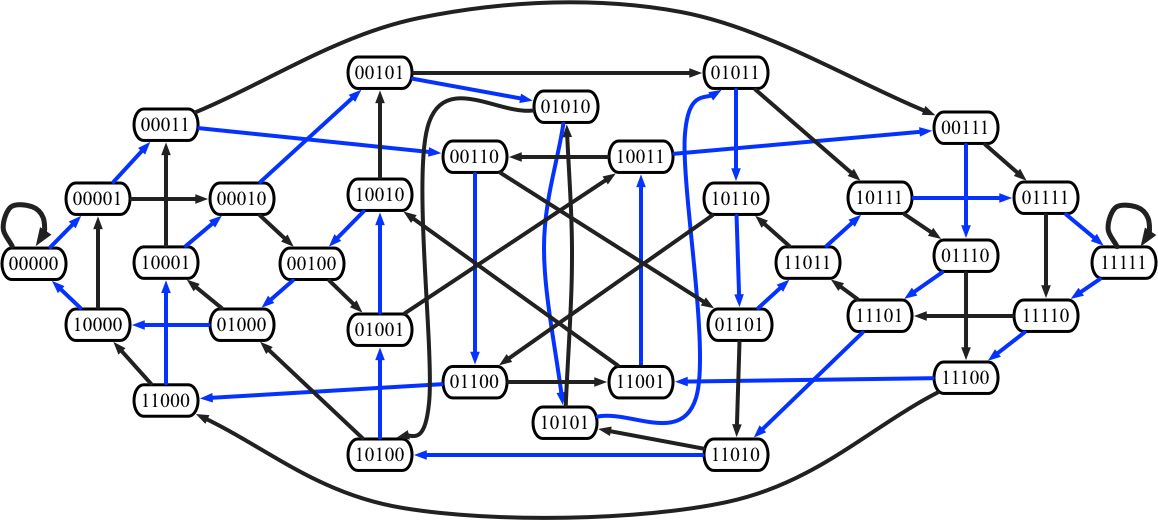
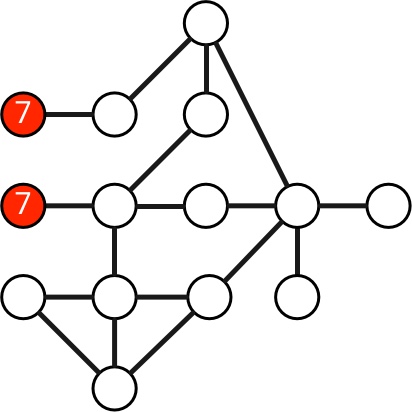
Jeux dans les graphes
Ce parcours propose de découvrir et d’expérimenter la notion de graphes et ses domaines d’application. Plusieurs variantes du parcours peuvent ainsi être proposées en fonction des thématiques souhaitées, de l’espace dédié, des supports disponibles (parcours composé de deux, trois ou quatre ateliers).
Niveau recommandé : à partir du cycle 2.
|
Jeu du Web surfeur – version plateau  Jeu de coloration – version plateau |
Jeu du Web surfeur – grandeur nature  Jeu de coloration – en ligne |
Plus court chemin – avec des trains  Jeu des gendarmes et du voleur |
Plus court chemin – grandeur nature Planification de tournées  Jeu des gendarmes et du voleur – en ligne |
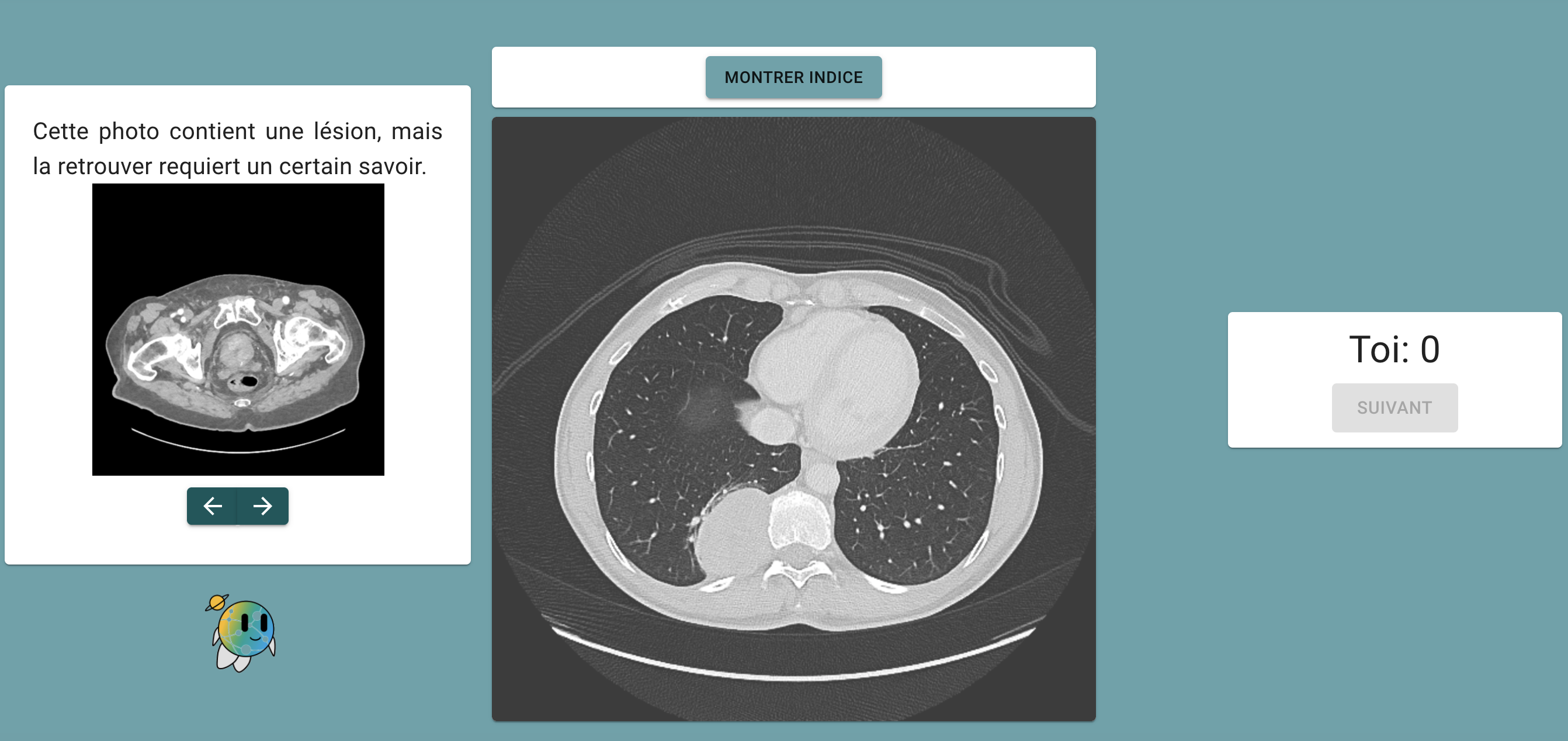
Sciences du numérique dans tous ses états
Ce parcours est un parcours orienté vers les usages des sciences du numérique : pour la conception de réseaux, pour l’imagerie médicale, pour la recommandation de contenus, pour se divertir, etc.
Niveau recommandé : à partir du cycle 3.
 IA pour l’imagerie médicale  Jeu datagramme |
 Conception d’un réseau téléphonique  Jeu biologie structurale computationnelle |
 Algorithmes de recommandation |
 Démonstrateur SameBot  Démonstrateur Puissance 4 |
Modélisation
Ce parcours permet de comprendre la notion de modélisation dans des domaines différents : environnements 3D, phénomènes naturels, réseaux de télécommunication, stabilité d’un pendule, plus court chemin dans un réseau routier, etc. Les ateliers proposés montreront aux visiteurs l’importance de la modélisation d’un problème pour sa future résolution. Plusieurs variantes du parcours peuvent être proposées en fonction des thématiques souhaitées ou de la durée de la session par exemple.
Niveau recommandé : à partir du cycle 3.
|
Jeu du Web surfeur – version plateau Apprentissage pour la stabilisation d’un pendule |
Jeu du Web surfeur – grandeur nature Plus court chemin – avec des trains |
 La science du ballon de foot  Géométrie sur écran sphérique |
 Construction d’un réseau routier |
Pavages : de Pythagore à l’IA
Ce parcours s’articule autour de la notion de pavages avec des ateliers sans ordinateur et d’autres avec des écrans originaux. Plusieurs variantes du parcours peuvent ainsi être proposées en fonction de l’espace dédié et des supports disponibles.
Niveau recommandé : à partir du cycle 3.
 Théorème du nid d’abeilles  Pavages |
Un puzzle qui résiste aux ordinateurs  Puzzle de Pythagore |
La science du ballon de foot |
Géométrie sur écran sphérique |
Géométrie et algorithmes
Ce parcours est composé d’ateliers dans lesquels la géométrie joue un rôle important (de manière directe ou plus subtilement dans les preuves de certains théorèmes notamment). Ces ateliers ont une composante algorithmique prononcée. Plusieurs variantes du parcours peuvent être proposées en fonction des thématiques souhaitées, entre autres.
Niveau recommandé : à partir du cycle 3.
|
Théorème du nid d’abeilles |
 Calcul d’enveloppe convexe Pavages |
 Contamination et preuve géométrique Puzzle de Pythagore |
 Goniométrie Solides de Platon et autres ateliers… |
Probabilités et numérique
Ce parcours propose de découvrir des ateliers dans lesquels la notion de probabilité est présente. Par exemple, des algorithmes peuvent être expérimentés par les visiteurs afin de comprendre comment les probabilités servent à la conception et l’analyse de certains algorithmes ou jeux.
Niveau recommandé : à partir du cycle 3.
|
Algorithmes de recommandation |
 Misez sur la bonne case |
IA pour gagner au jeu de Nim |
 Monty Hall |
Binaire
Ce parcours permet d’expérimenter de manière ludique la manière dont les ordinateurs comptent et comment les données sont représentées dans le monde numérique. Plusieurs variantes du parcours peuvent être proposées en mettant par exemple l’accent sur les tours de magie ou sur des ateliers de manipulation.
Niveau recommandé : à partir du cycle 3.
 Bracelet binaire |
 Compter en binaire |
 Transmission de pensée |
 Transmission d’images  La magie des graphes et du binaire |
Algorithmes
Ce parcours s’articule autour d’un des quatre piliers de l’informatique : les algorithmes. Les ateliers permettent de comprendre cette notion, de jouer avec et d’expérimenter des applications concrètes. Plusieurs variantes du parcours peuvent être proposées car un large ensemble d’ateliers sont disponibles. Cela en fonction de l’espace dédié, des thématiques, etc.
Niveau recommandé : à partir du cycle 2.
 Voyageur de commerce – version plateau  Parcours dans les graphes  Artistes peintres dans les graphes |
 Parcours dans les graphes – grandeur nature  Tours de Hanoï  Recherche dichotomique |
Plus court chemin – avec des trains  Coloration – version plateau en bois  LightsOut |
Plus court chemin – grandeur nature Planification de tournées Tri de cartes et autres ateliers… |
Fondements des sciences du numérique
Ce parcours propose des ateliers pour aborder les fondements mathématiques et informatiques des sciences du numérique : modélisation, système binaire, algorithmes, programme informatique, etc. Plusieurs variantes du parcours peuvent être proposées en fonction notamment des notions privilégiés.
Niveau recommandé : à partir du cycle 2.
 TableTop Transmission d’images  Réseau de tri – grandeur nature |
TaxiBot  Réseau de tri |
Compter en binaire  Sept ponts de Königsberg |
 Turing Tumble |
Magie
Ce parcours propose des ateliers qui ont en commun la magie comme accroche. Les notions abordées sont le système binaire, les preuves mathématiques, les invariants, les graphes notamment.
Niveau recommandé : à partir du cycle 3.
|
Transmission de pensée |
La magie des graphes et du binaire |
 Pouce magique |
 Compter en binaire |
Véhicules
Ce parcours permet d’aborder le thème des voitures avec des ateliers de nature différente : de la reconnaissance de formes à la robotique, des algorithmes à l’automatique. Plusieurs variantes du parcours peuvent être proposées en fonction notamment des applications souhaitées ou de l’espace dédié par exemple.
Niveau recommandé : à partir du cycle 3.
|
CreaCube Planification de tournées |
Optimisation des bus scolaires |
Plus court chemin – avec des trains |
TaxiBot |
Échecs
Ce parcours regroupe trois ateliers qui mettent lumière des notions différentes comme les stratégies d’un jeu, la modélisation, la combinatoire, les algorithmes (d’intelligence artificielle), etc.
Niveau recommandé : à partir du cycle 3.
 Chess Insight |
 N-queens |
Algorithmes pour les échecs |
Expériences scientifiques (robotisées)
Ce parcours regroupe un ensemble d’ateliers fabriqués avec du bois et robotisés. Ils permettent de (re)découvrir de belles expériences scientifiques.
Niveau recommandé : à partir du cycle 2.
 Plan incliné de Galilée robotisé |
 Planche de Galton |
 Brachistochrone robotisé |
